8 min to read

WaveParticle 水体渲染：波形渲染

Featured image

Wave Particle

思路

制作流程

分为了4个Pass。第一个Pass计算波粒子位置，并储存Amplitude。第二个Pass计算X方向（U）的Gradient和Displacement。第三个Pass计算Y（V）方向，生成最后的Gradient map和Displacement Map。第四个Pass用Gradient计算法线。 参考神秘海域4，我打算将4层不同频率的波粒子组合起来，为了减少render target的使用，我将4层水波分别放在了4个象限。 （对于Compute shader的调用，参考UE官方文档）

1.波粒子位置

这个Pass里一个粒子一个用一个Thread进行处理，将粒子的Amplitude储存进对应Render target的位置。一开始我是用的float格式的RT，但会出现多个波粒子重合时，Amplitude闪烁的情况。这是因为多个Thread在向同一个RT的像素点写入，产生了竞争关系，导致最后使用的Amplitude处于一个不可控的情况。解决办法就是位置信息的RT用uint格式，并且使用InterlockedAdd()确保一次只有一个粒子写入一个RT位置，用uint8的话会出现一些tilling上的问题，于是我用了uint32。 因为不同的层要放到不同的象限，所以我要对写入的位置做一些处理，我首先确认粒子能在0-1的UV空间当中循环，然后乘RT的分辨率，确定写入的纹素点。这里的RT分辨率要使用RT分辨率的1/2，要判断当前在哪个象限，最后写入的时候还要再加上不同象限的offset:

// write to the quarant
int2 quadrantOffset = int2((quadrant % 2) * Res, (quadrant / 2) * Res);

后面计算Gradient和Displacement的时候也要用到类似操作。 因为后续是从RT读取位置信息，每一帧读来的间隔会比较大，后面做出来的水波效果就是非连续的，会有一点卡顿感，于是我在写入的时候做一个类似双线性差值的操作，或者说反向双线性差值，就是将一个粒子的值分散到临近的4个纹素点里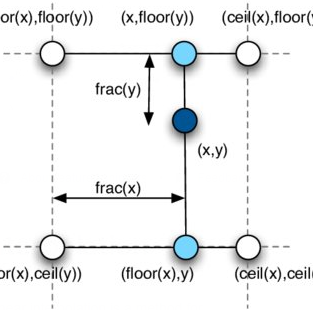 用临近点到实际点的距离作为Amplitude权重，这样后续计算的时候会考虑到这四个点的影响，水波移动起来的时候会平滑很多。

    // from UV to Texture sized space
    float2 texPos = newPos * (Res - 1);
    int2 baseCoord = int2(floor(texPos));
    float2 fracCoord = texPos - baseCoord; // use frac as weight

    // 4 pixels
    int2 coord0 = baseCoord;
    int2 coord1 = baseCoord + int2(1, 0);
    int2 coord2 = baseCoord + int2(0, 1);
    int2 coord3 = baseCoord + int2(1, 1);

    // weight (base on the distance to the center)
    float w0 = (1 - fracCoord.x) * (1 - fracCoord.y); // top left
    float w1 = fracCoord.x * (1 - fracCoord.y); // top right
    float w2 = (1 - fracCoord.x) * fracCoord.y; // bottom left
    float w3 = fracCoord.x * fracCoord.y; // bottom right

最后我再应用对应象限的offset写入权重之后的Amplitude。

uint quantizedAmplitude = (uint)(Particle.TransverseAmplitude * 100.0f);
uint4 splitAmplitude = uint4(
  quantizedAmplitude * w0,
  quantizedAmplitude * w1,
  quantizedAmplitude * w2,
  quantizedAmplitude * w3
);

    // write to the quarant
int2 quadrantOffset = int2((quadrant % 2) * Res, (quadrant / 2) * Res);
    InterlockedAdd(OutputPositionMapRT[coord0 % Res + quadrantOffset], splitAmplitude.x);
    InterlockedAdd(OutputPositionMapRT[coord1 % Res + quadrantOffset], splitAmplitude.y);
    InterlockedAdd(OutputPositionMapRT[coord2 % Res + quadrantOffset], splitAmplitude.z);
    InterlockedAdd(OutputPositionMapRT[coord3 % Res + quadrantOffset], splitAmplitude.w);
2.计算X方向（U）的Gradient和Displacement

接下来就要利用Amplitude和粒子的位置计算波形，大致就是用波形的公式作为Filter，读取位置和amplitude进行卷积。因为不管是垂直方向或者水平方向的位移/Gradient都需要在位置RT计算U和V（X,Y）方向的卷积，将卷积filter分成几个1D卷积核，这个pass只处理U/X方向，下个Pass就只处理V/Y方向。我参考了wave particle作者提供的近似公式（卷积核）。

Displacement

对于垂直方向的位移使用： \(dz(p) \approx d^X_z(x) \cdot d^Y_z(y)\)

\[d^{X}_z(x) = \frac{1}{2} \left( \cos \left( \frac{\pi x}{r} \right) + 1 \right) \Pi \left( \frac{x}{2r} \right)\] \[d^{Y}_z(y) = \frac{1}{2} \left( \cos \left( \frac{\pi y}{r} \right) + 1 \right) \Pi \left( \frac{y}{2r} \right)\]

这个Pass里只计算U(x)方向，也就是$d^{X}_z(x)$，再乘上从上一个pass中读到的amplitude， 对于水平的位移使用：

\[d_x(p) \approx d^X_x(x) \cdot d^Y_x(y)\] \[d_y(p) \approx d^X_y(x) \cdot d^Y_y(y)\] \[d_{x}^{X}(x) = -\frac{1}{2} \sin\left( \frac{\pi x}{r} \right) (\cos\left( \frac{\pi x}{r} \right) + 1) \prod\left( \frac{x}{2r} \right)\] \[d_{x}^{Y}(y) = \frac{1}{4} (\cos\left( \frac{\pi y}{r} \right) + 1)^2 \prod\left( \frac{y}{2r} \right)\] \[d_{y}^{Y}(y) = -\frac{1}{2} \sin\left( \frac{\pi y}{r} \right) (\cos\left( \frac{\pi y}{r} \right) + 1) \prod\left( \frac{y}{2r} \right)\] \[d_{y}^{X}(x) = \frac{1}{4} (\cos\left( \frac{\pi x}{r} \right) + 1)^2 \prod\left( \frac{x}{2r} \right)\]

因为水平的两个方向都要在U和V方向做计算，这里使用dXx和dYx。同时对于影响水平分量的公式,将sin/cos前方乘的公式中的amplitude替换为用户可以设定的值beta（0-1），这样的话就可以控制波的尖锐程度。同时用一个参数控制水平位移的强度。

Gradient

Gradient用来做之后的法线贴图，要同时考虑水平和垂直的gradient，也是使用作者提供的近似卷积核。 卷积代码在下方，可以看到我在半径的范围内进行卷积，并且保证tilling和象限。

for(int dx = -r; dx <= r; dx++)
{
	// looping and avoid negative value
	int PixelX = (RTCoord.x + Res + dx) % (Res);
	float amplitude = (float)InputPositionMapRT[int2(PixelX, RTCoord.y) + quadrantOffset] / 100.0f;

	// x
	float weightX = 0.5 * (cos(PI * dx / r) + 1) * (abs(dx) <= r ? 1 : 0);
	float dz = weightX * amplitude;

	// H Deviation
	float dxx = HDLevelParams[quadrant].Beta * sin(PI * dx / r) * (cos(PI * dx / r) + 1) * (abs(dx) <= r ? 1 : 0);
	float dyx = 0.25 * pow(cos(PI * dx / r) + 1, 2) * (abs(dx) <= r ? 1 : 0);
	
	sum.x += dxx * amplitude * HDLevelParams[quadrant].LongitudinalDirectionAmount.x;
	sum.y += dyx * amplitude * HDLevelParams[quadrant].LongitudinalDirectionAmount.y;
	sum.z += dz;

	// H Gradient
	float hxx =  HDLevelParams[quadrant].Beta * (cos(2 * PI * dx / r) + cos(PI * dx / r)) * (PI / r) * HDLevelParams[quadrant].LongitudinalDirectionAmount.x; // For HDeviation
	float hyx = 0.25 * pow(cos(PI * dx / r) + 1, 2)  * HDLevelParams[quadrant].LongitudinalDirectionAmount.x;
	float gxx =  -0.5 * sin(PI * dx / r) * (PI / r) * amplitude;
	float gyx = 0.5 * (cos(PI * dx / r) + 1)  * amplitude;
	sum_gradient += float4(hxx, hyx, gxx, gyx);
}
3.计算Y方向（V）的Gradient和Displacement

和上一个Pass相同，但是计算V方向，同时整合Gradient和Displacement（点积）。最后得到gradient和位移贴图。

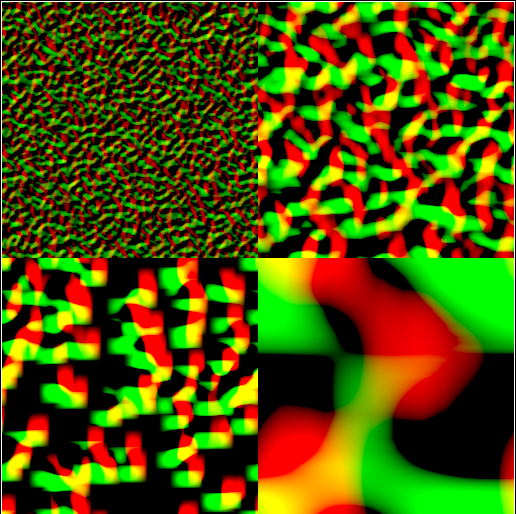
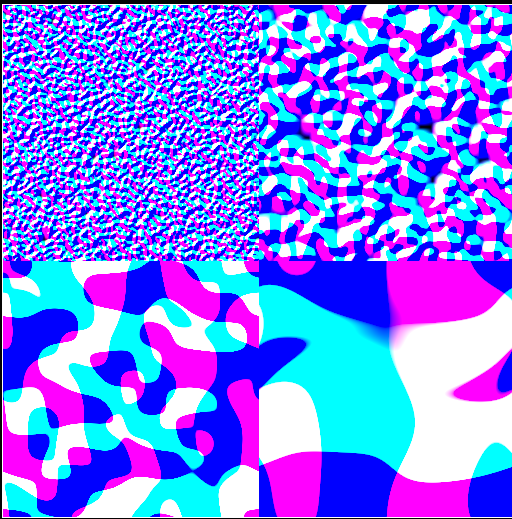
4.处理法线贴图

最后将Gradient作为法线的xy，再处理一下负值(也可以不用，这样之后可以在UE材质里直接使用)，就能得到法线了：

[numthreads(THREADS_X, THREADS_Y, THREADS_Z)]  
void ComputeNormalCS(uint3 DispatchId : SV_DispatchThreadID)  
{  
    float3 normal = 0;  
    normal.x = InputGradientMapRT[int2(DispatchId.x, DispatchId.y)].x;  
    normal.y = InputGradientMapRT[int2(DispatchId.x, DispatchId.y)].y;  
    normal.z = 1.0f;  
    normal = normalize(normal);  
    normal = (normal + 1.0f) / 2.0f;  
  
    OutputNormalMapRT[DispatchId.xy] = float4(normal, 1.0f);  

}

结果